6. Kernel Methods¶
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from prml.kernel import (
PolynomialKernel,
RBF,
GaussianProcessClassifier,
GaussianProcessRegressor
)
def create_toy_data(func, n=10, std=1., domain=[0., 1.]):
x = np.linspace(domain[0], domain[1], n)
t = func(x) + np.random.normal(scale=std, size=n)
return x, t
def sinusoidal(x):
return np.sin(2 * np.pi * x)
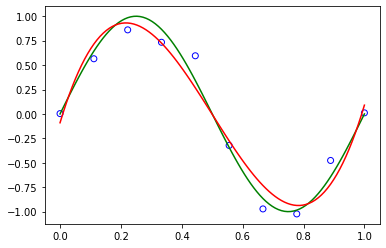
6.1 Dual Representation¶
x_train, y_train = create_toy_data(sinusoidal, n=10, std=0.1)
x = np.linspace(0, 1, 100)
model = GaussianProcessRegressor(kernel=PolynomialKernel(3, 1.), beta=int(1e10))
model.fit(x_train, y_train)
y = model.predict(x)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", color="blue", label="training")
plt.plot(x, sinusoidal(x), color="g", label="sin$(2\pi x)$")
plt.plot(x, y, color="r", label="gpr")
plt.show()
6.4 Gaussian Processes¶
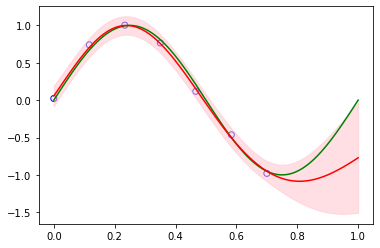
6.4.2 Gaussian processes for regression¶
x_train, y_train = create_toy_data(sinusoidal, n=7, std=0.1, domain=[0., 0.7])
x = np.linspace(0, 1, 100)
model = GaussianProcessRegressor(kernel=RBF(np.array([1., 15.])), beta=100)
model.fit(x_train, y_train)
y, y_std = model.predict(x, with_error=True)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", color="blue", label="training")
plt.plot(x, sinusoidal(x), color="g", label="sin$(2\pi x)$")
plt.plot(x, y, color="r", label="gpr")
plt.fill_between(x, y - y_std, y + y_std, alpha=0.5, color="pink", label="std")
plt.show()
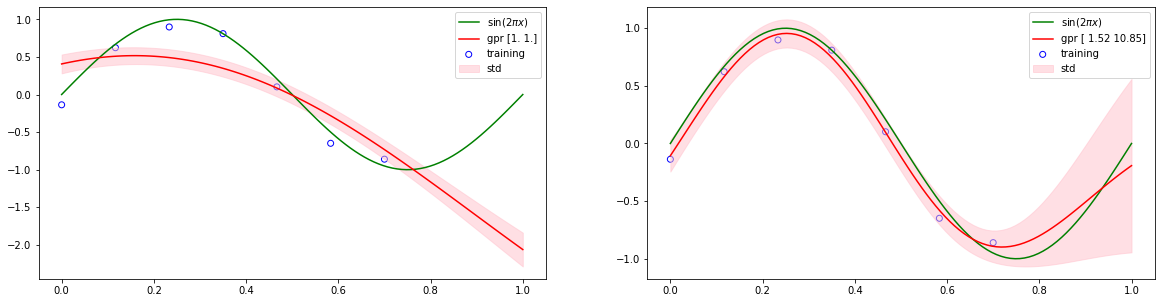
6.4.3 Learning the hyperparameters¶
x_train, y_train = create_toy_data(sinusoidal, n=7, std=0.1, domain=[0., 0.7])
x = np.linspace(0, 1, 100)
plt.figure(figsize=(20, 5))
plt.subplot(1, 2, 1)
model = GaussianProcessRegressor(kernel=RBF(np.array([1., 1.])), beta=100)
model.fit(x_train, y_train)
y, y_std = model.predict(x, with_error=True)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", color="blue", label="training")
plt.plot(x, sinusoidal(x), color="g", label="sin$(2\pi x)$")
plt.plot(x, y, color="r", label="gpr {}".format(model.kernel.params))
plt.fill_between(x, y - y_std, y + y_std, alpha=0.5, color="pink", label="std")
plt.legend()
plt.subplot(1, 2, 2)
model.fit(x_train, y_train, iter_max=100)
y, y_std = model.predict(x, with_error=True)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", color="blue", label="training")
plt.plot(x, sinusoidal(x), color="g", label="sin$(2\pi x)$")
plt.plot(x, y, color="r", label="gpr {}".format(np.round(model.kernel.params, 2)))
plt.fill_between(x, y - y_std, y + y_std, alpha=0.5, color="pink", label="std")
plt.legend()
plt.show()
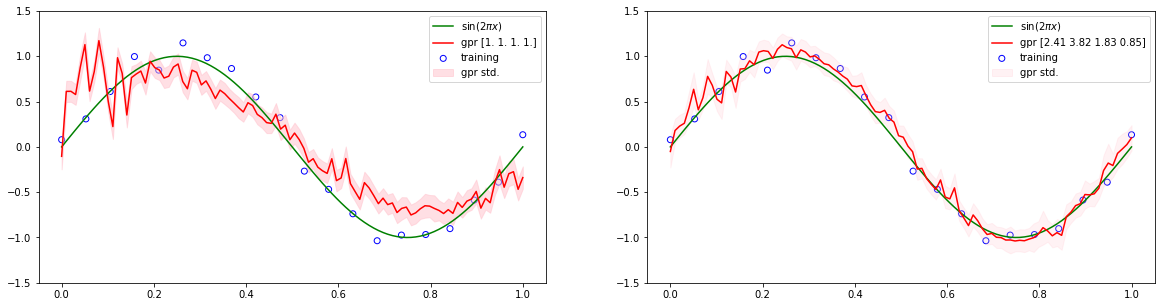
6.4.4 Automatic relevance determination¶
def create_toy_data_3d(func, n=10, std=1.):
x0 = np.linspace(0, 1, n)
x1 = x0 + np.random.normal(scale=std, size=n)
x2 = np.random.normal(scale=std, size=n)
t = func(x0) + np.random.normal(scale=std, size=n)
return np.vstack((x0, x1, x2)).T, t
x_train, y_train = create_toy_data_3d(sinusoidal, n=20, std=0.1)
x0 = np.linspace(0, 1, 100)
x1 = x0 + np.random.normal(scale=0.1, size=100)
x2 = np.random.normal(scale=0.1, size=100)
x = np.vstack((x0, x1, x2)).T
model = GaussianProcessRegressor(kernel=RBF(np.array([1., 1., 1., 1.])), beta=100)
model.fit(x_train, y_train)
y, y_std = model.predict(x, with_error=True)
plt.figure(figsize=(20, 5))
plt.subplot(1, 2, 1)
plt.scatter(x_train[:, 0], y_train, facecolor="none", edgecolor="b", label="training")
plt.plot(x[:, 0], sinusoidal(x[:, 0]), color="g", label="$\sin(2\pi x)$")
plt.plot(x[:, 0], y, color="r", label="gpr {}".format(model.kernel.params))
plt.fill_between(x[:, 0], y - y_std, y + y_std, color="pink", alpha=0.5, label="gpr std.")
plt.legend()
plt.ylim(-1.5, 1.5)
model.fit(x_train, y_train, iter_max=100, learning_rate=0.001)
y, y_std = model.predict(x, with_error=True)
plt.subplot(1, 2, 2)
plt.scatter(x_train[:, 0], y_train, facecolor="none", edgecolor="b", label="training")
plt.plot(x[:, 0], sinusoidal(x[:, 0]), color="g", label="$\sin(2\pi x)$")
plt.plot(x[:, 0], y, color="r", label="gpr {}".format(np.round(model.kernel.params, 2)))
plt.fill_between(x[:, 0], y - y_std, y + y_std, color="pink", alpha=0.2, label="gpr std.")
plt.legend()
plt.ylim(-1.5, 1.5)
plt.show()
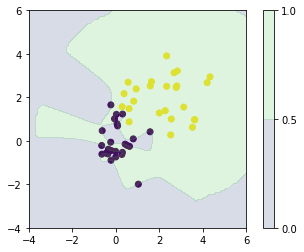
6.4.5 Gaussian processes for classification¶
def create_toy_data():
x0 = np.random.normal(size=50).reshape(-1, 2)
x1 = np.random.normal(size=50).reshape(-1, 2) + 2.
return np.concatenate([x0, x1]), np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)[:, None]
x_train, y_train = create_toy_data()
x0, x1 = np.meshgrid(np.linspace(-4, 6, 100), np.linspace(-4, 6, 100))
x = np.array([x0, x1]).reshape(2, -1).T
model = GaussianProcessClassifier(RBF(np.array([1., 7., 7.])))
model.fit(x_train, y_train)
y = model.predict(x)
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train.ravel())
plt.contourf(x0, x1, y.reshape(100, 100), levels=np.linspace(0,1,3), alpha=0.2)
plt.colorbar()
plt.xlim(-4, 6)
plt.ylim(-4, 6)
plt.gca().set_aspect('equal', adjustable='box')