Accept / Reject Monte Carlo¶
import numpy as np
import matplotlib.pyplot as plt
#this is an example distribution, feel free to change it
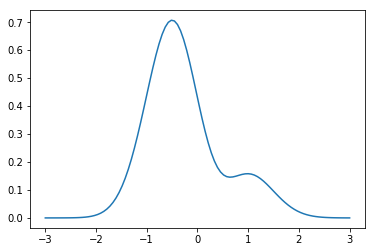
def p(x):
return np.sin(x-0.5)**2 * np.exp(-x**2) + .2*np.exp(-x**2) #note, this one is not normalized pdf
#let's plot it
x = np.linspace(-3,3,100)
y = p(x)
plt.plot(x,y)
[<matplotlib.lines.Line2D at 0x118cfe2b0>]
native python accept / reject¶
This is meant to be an easily readable implementation of the accept / reject algorithm. It’s easy to understand not very fast.
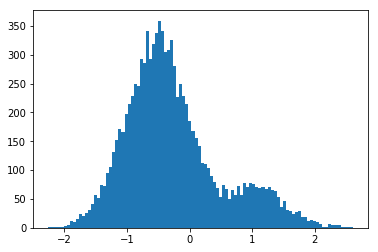
def accept_reject(N):
xmin = -3
xmax = 3
pmax = 0.8
n_accept=0
x_list = []
while n_accept < N:
t = (xmax-xmin)*np.random.rand() + xmin
y = np.random.rand()
if y < p(t)/ pmax:
n_accept += 1
x_list.append(t)
return x_list
x = accept_reject(10000)
bins, edges, patches = plt.hist(x, bins=100)
A faster numpy implementation¶
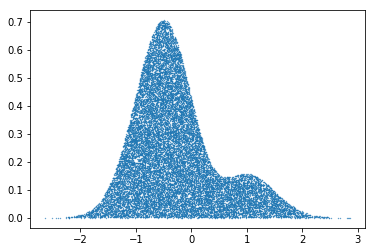
xmin = -3
xmax = 3
pmax = 0.8
N_MC = 100000
t = np.random.uniform(xmin,xmax,N_MC) #get uniform temporary x values
y = np.random.uniform(0,pmax,N_MC) # get uniform random y values
# plot all the t-y pairs
plt.scatter(t,y, s=0.1, c='orange')
<matplotlib.collections.PathCollection at 0x118ee7da0>

#make a mask that keeps index to the accepted pairs. Plot them
mask = y<p(t)
plt.scatter(t[mask],y[mask], s=0.1)
<matplotlib.collections.PathCollection at 0x11929f6a0>
#inspect the mask
mask
array([False, False, False, ..., False, False, False], dtype=bool)
#inspect the 0th entry
t[0], y[0], p(t[0]), mask[0]
(0.5344133723538036, 0.43914651222070833, 0.15120270124751428, False)
#How many t's are there beore / after the mask
t.size, t[mask].size
(100000, 22015)
accept_prob = t[mask].size/t.size
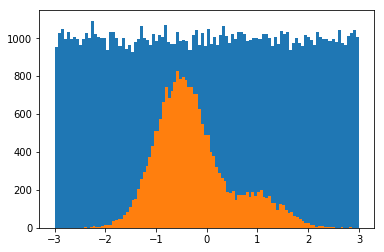
#histogram the t values with and without the mask
_ = plt.hist(t, bins=100)
_ = plt.hist(t[mask], bins=100)
compare speed of the two approaches¶
%%timeit
xmin = -3
xmax = 3
pmax = 0.8
N_MC = 100000
t = np.random.uniform(xmin,xmax,N_MC) #get uniform temporary x values
y = np.random.uniform(0,pmax,N_MC) # get uniform random y values
mask = y<p(t)
5.56 ms ± 71 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
%%timeit
N_MC = 100000
#for a fair comparison, we will ask accept_reject to return the same number
average_accept = N_MC*accept_prob
x = accept_reject(average_accept)
564 ms ± 94 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
#How much faster?
564/5.56
101.43884892086332
