Independence¶
As discussed in the previous section, conditional probabilities quantify the extent to which the knowledge of the occurrence of a certain event affects the probability of another event 1. In some cases, it makes no difference: the events are independent. More formally, events \(A\) and \(B\) are independent if and only if
This definition is not valid if \(P (B) = 0\). The following definition covers this case and is otherwise equivalent.
Definition (Independence).
Let \((\Omega,\mathcal{F},P)\) be a probability space. Two events \(A,B \in \mathcal{F}\) are independent if and only if
Notation
This is often denoted \( A \indep B \)
Similarly, we can define conditional independence between two events given a third event. \(A\) and \(B\) are conditionally independent given \(C\) if and only if
where \(P (A|B, C) := P (A|B \cap C)\). Intuitively, this means that the probability of \(A\) is not affected by whether \(B\) occurs or not, as long as \(C\) occurs.
Notation
This is often denoted \( A \indep B \mid C\)
Graphical Models¶
There is a graphical model representation for joint distributions \(P(A,B,C)\) that encodes their conditional (in)dependence known as a probabilistic graphical model. For this situation \( A \indep B \mid C\), the graphical model looks like this:
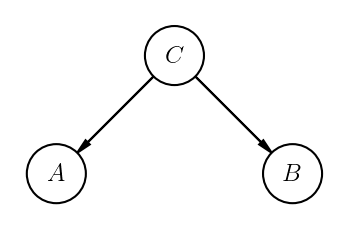
The lack of an edge directly between \(A\) and \(B\) indicates that the two varaibles are conditionally independent. This image was produced with daft, and there are more examples in Visualizing Graphical Models.
- 1
This text is based on excerpts from Section 1.3 of NYU CDS lecture notes on Probability and Statistics
