Contents

Visualizing Graphical Models

Here we use daft by David S. Fulford, Dan Foreman-Mackey and David W. Hogg to visualize probabilistic graphical models .

For more on graphical models:

  1. Foundations of Graphical Models by David Blei – see Basics of Graphical Models

    1. see also a video on d-separation by Pieter Abbeel

    2. semantics of graphical models (called “Boiler plate diagrams” in the tech report) and an extended visual language Directed Factor Graph Notation for Generative Models Laura Dietz, which is the basis of the tikz-bayesnet package

import daft
from matplotlib import rc

rc("font", family="serif", size=12)
rc("text", usetex=True)

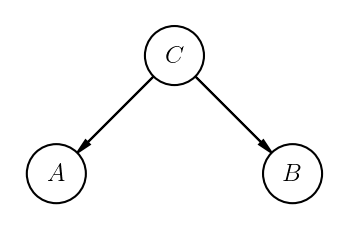
Conditional independence

Random variables \(A\) and \(B\) are conditionally independent given \(C\) if and only if

(31)\[\begin{equation} P (A|B, C) = P (A|C) , \end{equation}\]

This is often written \( A \perp\kern-5pt\perp B \mid C\). The graphical model for this situation looks like this:

pgm = daft.PGM()
pgm.add_node("A", r"$A$", -1, 0)
pgm.add_node("B", r"$B$", 1, 0)
pgm.add_node("C", r"$C$", 0, 1)
pgm.add_edge("C", "A")
pgm.add_edge("C", "B")
pgm.render(dpi=150)
pgm.savefig("../assets/AperpBmidC.png", dpi=150)
../_images/daft_3_0.png

An weak lensing example

Origin of Weak Lensing Example

pgm = daft.PGM()
pgm.add_node("Omega", r"$\Omega$", -1, 4)
pgm.add_node("gamma", r"$\gamma$", 0, 4)
pgm.add_node("obs", r"$\epsilon^{\mathrm{obs}}_n$", 1, 4, observed=True)
pgm.add_node("alpha", r"$\alpha$", 3, 4)
pgm.add_node("true", r"$\epsilon^{\mathrm{true}}_n$", 2, 4)
pgm.add_node("sigma", r"$\sigma_n$", 1, 3)
pgm.add_node("Sigma", r"$\Sigma$", 0, 3)
pgm.add_node("x", r"$x_n$", 2, 3, observed=True)
pgm.add_plate([0.5, 2.25, 2, 2.25], label=r"galaxies $n$")
pgm.add_edge("Omega", "gamma")
pgm.add_edge("gamma", "obs")
pgm.add_edge("alpha", "true")
pgm.add_edge("true", "obs")
pgm.add_edge("x", "obs")
pgm.add_edge("Sigma", "sigma")
pgm.add_edge("sigma", "obs")

pgm.render(dpi=150)
#pgm.savefig("weaklensing.pdf")
#pgm.savefig("weaklensing.png", dpi=150)

<matplotlib.axes._axes.Axes at 0x7fafc93525b0>
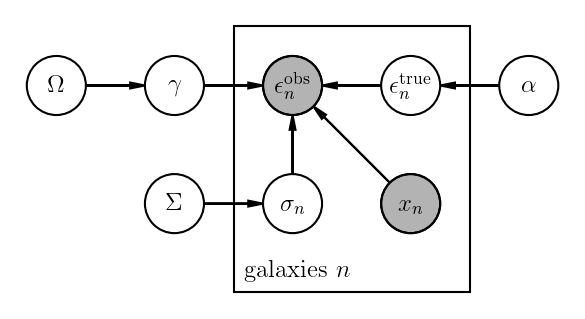
../_images/daft_5_1.png

This graphical model is equivalent to factorizing the joint distribution according to this equation:

\[ p(\Omega, \Sigma, \gamma, \alpha, \{\epsilon_n^\textrm{obs},\epsilon_n^\textrm{true} \sigma_n, x_n\} ) = \left[ \prod_n p(\epsilon_n^\textrm{obs} | x_n, \sigma_n, \epsilon_n^\textrm{true}, \gamma) p(\epsilon_n^\textrm{true}|\alpha) p(x_n) p(\sigma_n | \Sigma) \right ] p(\alpha) p(\Sigma) p(\gamma | \Omega) p(\Omega) \]

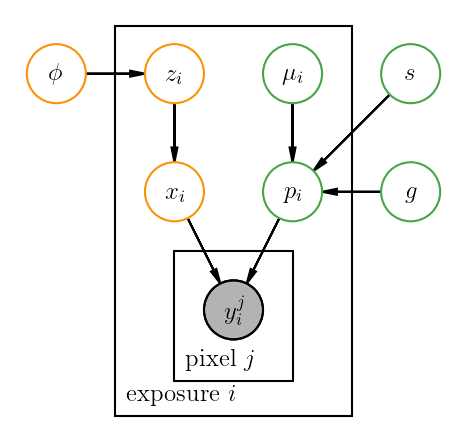
An exoplanets example

Origin of exoplanet example

# Colors.
p_color = {"ec": "#46a546"}
s_color = {"ec": "#f89406"}

pgm = daft.PGM()

n = daft.Node("phi", r"$\phi$", 1, 3, plot_params=s_color)
n.va = "baseline"
pgm.add_node(n)
pgm.add_node("speckle_coeff", r"$z_i$", 2, 3, plot_params=s_color)
pgm.add_node("speckle_img", r"$x_i$", 2, 2, plot_params=s_color)

pgm.add_node("spec", r"$s$", 4, 3, plot_params=p_color)
pgm.add_node("shape", r"$g$", 4, 2, plot_params=p_color)
pgm.add_node("planet_pos", r"$\mu_i$", 3, 3, plot_params=p_color)
pgm.add_node("planet_img", r"$p_i$", 3, 2, plot_params=p_color)

pgm.add_node("pixels", r"$y_i ^j$", 2.5, 1, observed=True)

# Edges.
pgm.add_edge("phi", "speckle_coeff")
pgm.add_edge("speckle_coeff", "speckle_img")
pgm.add_edge("speckle_img", "pixels")

pgm.add_edge("spec", "planet_img")
pgm.add_edge("shape", "planet_img")
pgm.add_edge("planet_pos", "planet_img")
pgm.add_edge("planet_img", "pixels")

# And a plate.
pgm.add_plate([1.5, 0.2, 2, 3.2], label=r"exposure $i$", shift=-0.1)
pgm.add_plate([2, 0.5, 1, 1], label=r"pixel $j$", shift=-0.1)

# Render and save.
pgm.render(dpi=150)
#pgm.savefig("exoplanets.pdf")
#pgm.savefig("exoplanets.png", dpi=150)

<matplotlib.axes._axes.Axes at 0x7fafc93af100>
../_images/daft_8_1.png
An interactive exploration of statistical fluctuations in histograms Statistics Topics