An example with with autodiff
import numpy as np
import scipy.stats as scs
import matplotlib.pyplot as plt
mean=1.
std = .3
N = 10000
x = np.random.normal(mean, std, N)
x_plot = np.linspace(0.1,3,100)
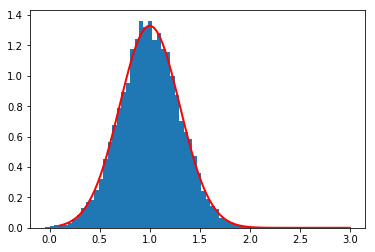
_ = plt.hist(x, bins=50, density=True)
plt.plot(x_plot, scs.norm.pdf(x_plot, mean, std), c='r', lw=2)
def q(x):
return 1/x
q_ = q(x)
q_plot = q(x_plot)
plt.plot(x_plot, q_plot,label='q(x)')
_ = plt.hist(x, bins=50, density=True, label='p(x)')
plt.xlabel('x')
plt.ylabel('q or p(q)')
plt.legend()
mybins = np.linspace(0,3,50)
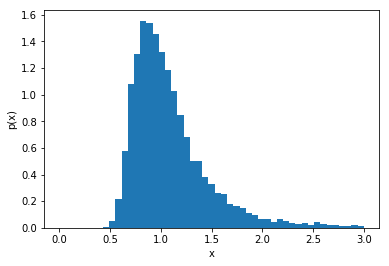
_ = plt.hist(q_, bins=mybins, density=True)
plt.xlabel('x')
plt.ylabel('p(x)')
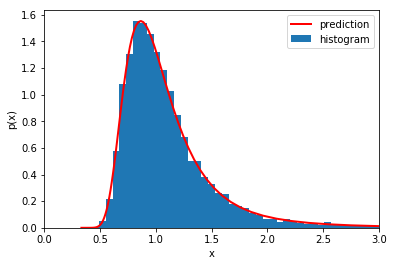
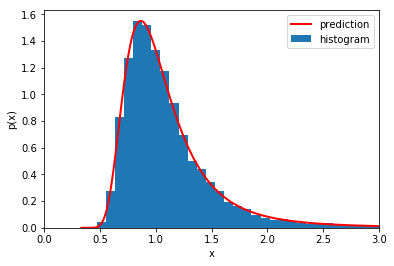
_ = plt.hist(q_, bins=mybins, normed=True, label='histogram')
plt.plot(q_plot, scs.norm.pdf(1/q_plot, mean, std)/q_plot/q_plot, c='r', lw=2, label='prediction')
plt.xlim((0,3))
plt.xlabel('x')
plt.ylabel('p(x)')
plt.legend()
Alternatively, we don't need to know how to invert $x(q)$. Instead, we can start with x_plot and use the evaluated pairs (x_plot, q_plot=q(x_plot)). Then we can just use x_plot when we want $x(q)$.
Here is a plot of the inverse mad ethat way.
plt.plot(q_plot, x_plot, c='r', lw=2, label='inverse x(q)')
plt.xlim((0,3))
plt.xlabel('q')
plt.ylabel('x(q)')
plt.legend()
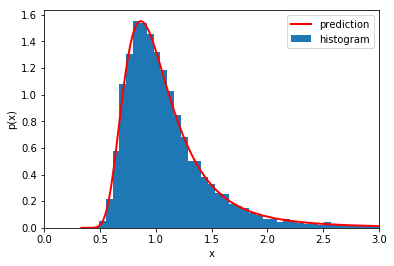
and here is a plot of our prediction using x_plot directly
_ = plt.hist(q_, bins=mybins, normed=True, label='histogram')
plt.plot(q_plot, scs.norm.pdf(x_plot, mean, std)/np.power(x_plot,-2), c='r', lw=2, label='prediction')
plt.xlim((0,3))
plt.xlabel('x')
plt.ylabel('p(x)')
plt.legend()
from jax import grad, vmap
import jax.numpy as np
#define the gradient with grad(q)
dq = grad(q) #dq is a new python function
print(dq(.5)) # should be -4
# dq(x) #broadcasting won't work. Gives error:
# Gradient only defined for scalar-output functions. Output had shape: (10000,).
#define the gradient with grad(q) that works with broadcasting
dq = vmap(grad(q))
#print dq/dx for x=0.5, 1, 2
# it should be -1/x^2 =. -4, 1, -0.25
dq( np.array([.5, 1, 2.]))
#plot gradient
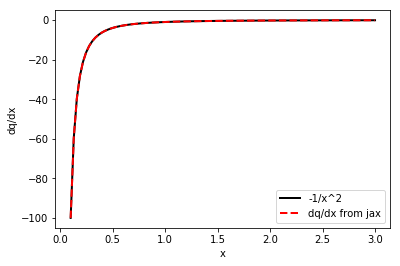
plt.plot(x_plot, -np.power(x_plot,-2), c='black', lw=2, label='-1/x^2')
plt.plot(x_plot, dq(x_plot), c='r', lw=2, ls='dashed', label='dq/dx from jax')
plt.xlabel('x')
plt.ylabel('dq/dx')
plt.legend()
We want to evaluate
$p_q(q) = \frac{p_x(x(q))}{ | dq/dx |} $,
which requires knowing how to invert from $q \to x$. That's easy, it's just $x(q)=1/q$. But we also have evaluated pairs (x_plot, q_plot), so we can just use x_plot when we want $x(q)$
Put it all together.
Again we can either invert x(q) by hand and use Jax for derivative:
_ = plt.hist(q_, bins=np.linspace(-1,3,50), density=True, label='histogram')
plt.plot(q_plot, scs.norm.pdf(1/q_plot, mean, std)/np.abs(dq(1/q_plot)), c='r', lw=2, label='prediction')
plt.xlim((0,3))
plt.xlabel('x')
plt.ylabel('p(x)')
plt.legend()
or we can use the pairs x_plot, q_plot
_ = plt.hist(q_, bins=np.linspace(-1,3,50), density=True, label='histogram')
plt.plot(q_plot, scs.norm.pdf(x_plot, mean, std)/np.abs(dq(x_plot)), c='r', lw=2, label='prediction')
plt.xlim((0,3))
plt.xlabel('x')
plt.ylabel('p(x)')
plt.legend()